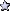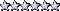We have been asked about how the box part of box plots are determined, particularly how the "hinges" are calculated. I couldn't find a detailed description, and it seems that there are several ways this can be done. Can you provide the formulations that TeeChart uses?
The conventional way of drawing box plots seems to be to draw the upper and lower boundaries at the 25th and 75th percentiles, and the median at the 50th percentile.
Our user's example data values (with rank underneath) is as follows:
(note: am using CODE here for formatting only)
Code: Select all
1 19 20 24 28 37 57 58 60 75 80
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11)- median (2nd quartile) = value 6 = 37
- 25th percentile (1st quartile) = value 3 = 20
- 75th percentile (3rd quartile) = value 9 = 60
However, the box plot we are getting seemingly puts the lower hinge at 21 and the upper at 59.5.
To illustrate, below I have plotted the ranked data values (over the character location number for reference), followed by the conventionally-expected boxplot and then the actual one:
Rank plot:
Code: Select all
X.................XX...X...X........X...................XX.X..............X....X
12345678901234567890123456789012345678901234567890123456789012345678901234567890Note: instead of '|' to symbolize the perimeter ends of the box, the lower case 'x' was used to indicate that it is an actual value in the input data.
Code: Select all
+----------------+----------------------+
X.................Xx...X...X........M...................XX.x..............X....X
+----------------+----------------------+Code: Select all
+---------------+---------------------+
X.................XX|..X...X........M...................XX|X..............X....X
+---------------+---------------------+ Formula
Based on some investigation of statistical resources on the web, I came across a method that seems to give the same results as that seen in TeeChart. I shall describe it here:
- We are looking for the values of the 25th and 75th percentiles (p = 25 and p = 75).
- The p-th percentile of N ordered values is obtained by first calculating the rank:
Code: Select all
Rp = N/100 * p + .5- If Rp is not an integer, a value must be calculated.
- First, the rank Rp is divided into the integer component k and the decimal component d.
- With these, the p-th percentile is calculated with:
Code: Select all
Vp = Rk + d * (R(k+1) - Rk)When this formula is applied to the dataset provided above, following are the calulculations and the results:
In the case of this dataset, N = 11.
25th percentile:
The ranked value of the 25th percentile is:
Code: Select all
R25 = 11 / 100 * 25 + .5
= .11 * 25 + .5
= 2.75 + .5
= 3.25For the 25th percentile,
Code: Select all
V25 = Rk + d * (R(k+1) - Rk)
where R3 = 20 and R4 = 24
= 20 + .25 * (24 - 20)
= 20 + .25 * 4
= 20 + 1
= 21The ranked value of the 75th percentile is:
Code: Select all
R75 = 11 / 100 * 75 + .5
= .11 * 75 + .5
= 8.25 + .5
= 8.75For the 75th percentile,
Code: Select all
V75 = Rk + d * (R(k+1) - Rk)
where R8 = 58 and R9 = 60
= 58 + .75 * (60 - 58)
= 58 + .75 * 2
= 58 + 1.5
= 59.5For a box plot drawn from this dataset, this formula puts the the lower hinge of the box at 21, and the upper hinge at value 59.5.
Thanks!
juan
(we are using v7.0.0.6, btw)